马克社区,马克吐温社区,马克java社区OpenLayers 和 turf.js 的灵异事件：什么？我画的圆居然不是圆！

OpenLayers 和 turf.js 的灵异事件：什么？我画的圆居然不是圆！

事情的起因：

使用ol.geom.Circle这个几何可以在OpenLayers中画一个圆形的要素，虽然我们知道它并不是OGC标准的要素类型。

昨天群友找我解决一个有意思的问题：使用投影EPSG：3857的时候，在用ol.geom.Circle画了一个圆形的要素之后，又用turf.circle在同样的位置，用同样的半径画了一个圆形的要素。

var fCircleBeta = new Feature({
  geometry: new Circle([4500000, 4500000], 1000000
  )
})
vCircleSource.addFeature(fCircleBeta);
 
 
 
var circle = turf.circle(toLonLat([4500000, 4500000]), 1000000, { steps: 100, units: 'meters' });
var turfCircleFeatureNorth = (new GeoJSON()).readFeature(circle, {
  dataProjection: "EPSG:4326",
  featureProjection: "EPSG:3857"
});
vCircleSource.addFeature(turfCircleFeatureNorth);

结果却变成了这样：

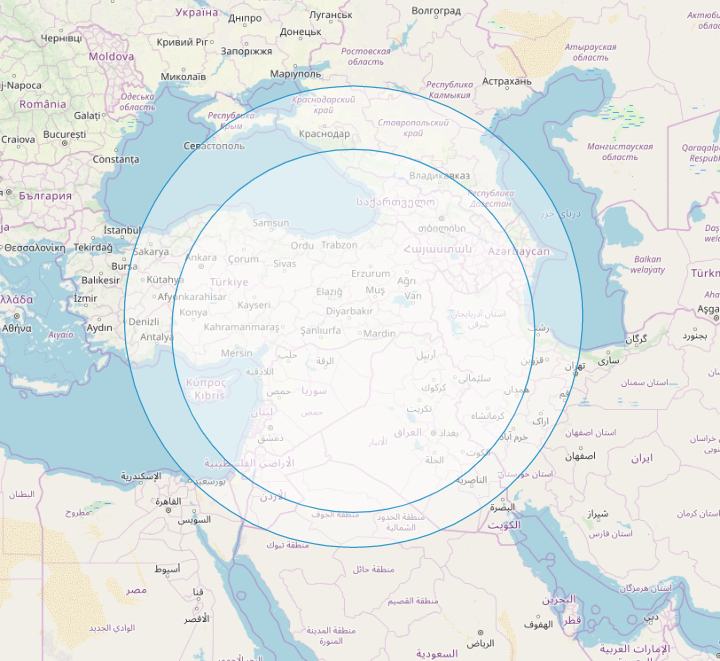
！！！这是什么情况？
事情的处理：

我仔细观察了一下，叫他以0,0为圆心，再分别画两个圆。

然后就是这个样子（为了方便区分，特意将turf的正多边形逼近的圆减少了边数）：

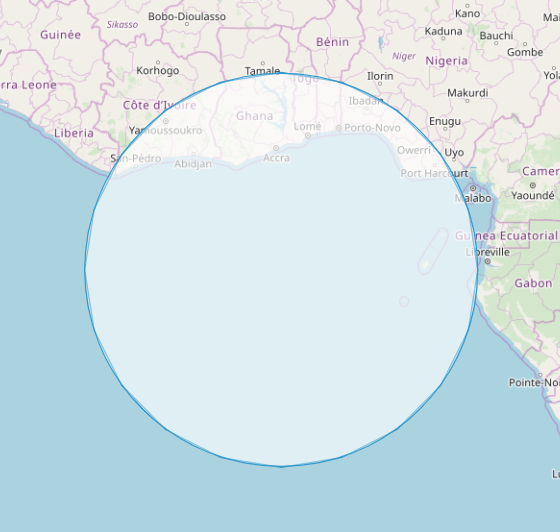
在这里插入图片描述

基本重合了。

所以至此基本可以得到结论：turf是按照球面画圆的，ol是按照平面画圆的，当按照3857投影坐标系进行投影后，越靠近北极，形变越大，所以turf画的圆就投影为一个上宽下窄的、胖了一圈的“圆”。

为了证明此事，我还需要做一个实验。
真相大白：

实验的思路就是，以第一组的两个圆为例，监听鼠标移动事件，显示鼠标位置到[4500000,4500000]的距离。当我把鼠标分别放到两个“圆”的边上面时，大略就能计算得到“半径”。借了两个控件，简单写了一个鼠标位置的popup：

var pointerMoveHandler = function (evt) {
  if (evt.dragging) {
    return;
  }
  let radiusFlat = Math.sqrt(Math.pow((evt.coordinate[0] - 4500000), 2) + Math.pow((evt.coordinate[1] - 4500000), 2));
  let radiusSphere = olSphere.getDistance(toLonLat([4500000, 4500000]), toLonLat(evt.coordinate));
  tooltipElement.innerHTML = "鼠标坐标：" + evt.coordinate + "</br>" + "平面距离：" + radiusFlat + "</br>" + "球面距离：" + radiusSphere + "</br>";
  helpTooltip.setPosition(evt.coordinate);
  tooltipElement.classList.remove('hidden');
};
map.on('pointermove', pointerMoveHandler);
 
function createHelpTooltip() {
  if (tooltipElement) {
    tooltipElement.parentNode.removeChild(tooltipElement);
  }
  tooltipElement = document.createElement('div');
  tooltipElement.className = 'tooltip hidden';
  helpTooltip = new Overlay({
    element: tooltipElement,
    offset: [15, 0],
    positioning: 'center-left'
  });
  map.addOverlay(helpTooltip);
}

然后就得到了下面的结果：
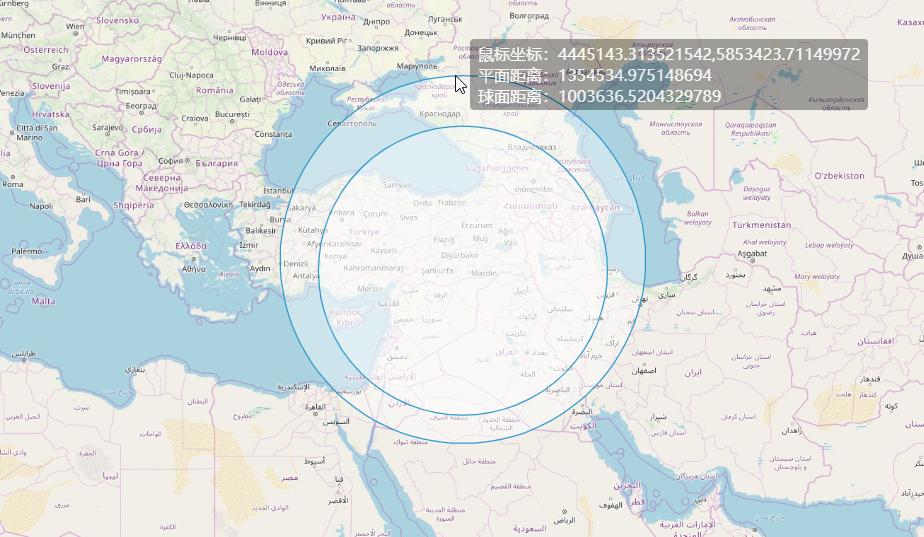
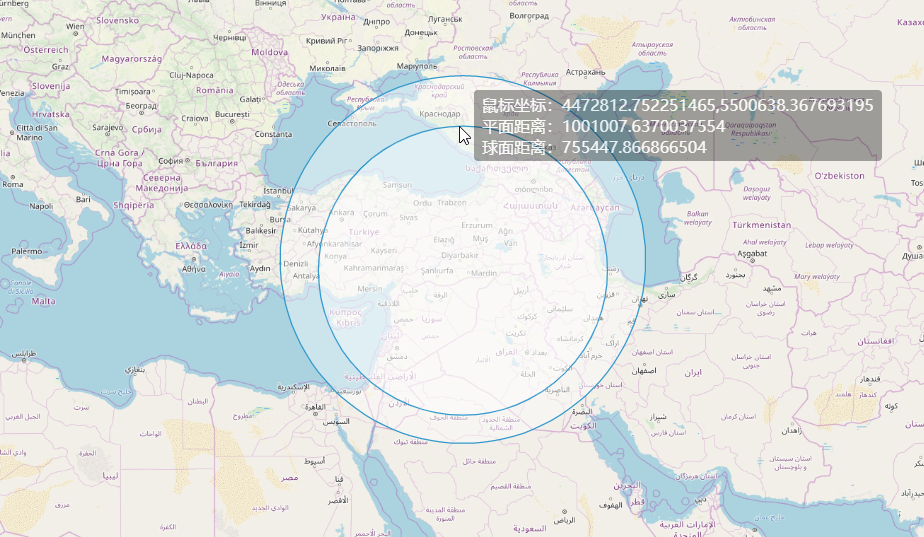
在这里插入图片描述

可见我的猜想是正确的。
结论：

并非灵异事件，只是绘制方法不同罢了。如果做空间分析，还是turf靠谱一点，毕竟是接近实地距离的。如果使用OpenLayers的ol.geom.Circle类，也不见得错，只不过受到了3857坐标系投影造成的误差影响罢了——尽管看上去它才是正“圆”，但是到实地去真实测量到圆心距离的话，一定是小于理想半径的。

其他