什么是梯度下降法与delta法则

马克-to-win @ 马克java社区：防盗版实名手机尾号：73203。梯度下降法就是沿梯度下降的方向求解函数（误差）极小值。delta法则是使用梯度下降法来找到最佳权向量。拿数字识别这个案例为例，训练模型的过程通常是这样的。输入为1万张图片，也就是1万个样本，我们定义为D，是训练样例集合，输出为相对应的1万个数字。马克-to-win @ 马克java社区：这就是1万个目标输出(Target），每一个目标输出我们定义为：td ，是训练样例d的目标输出。我们的模型训练的目的是想找出，此人工神经网络模型的参数，比如权向量w 等。要注意，目标输出td是已知的（非变量，比如5这张图，目标输出就是5这个数字），样本也是已知的。马克-to-win @ 马克java社区：参数是未知的。还有什么是未知的?这就需要从训练的过程入手了。训练过程，通常开始时，所有的权向量w都从一个很小的值开始，比如零， 这时有一个实际输出（od是对训练样例d的实际输出）。目标输出和实际输出的差距叫做误差。因为一共有1万个样本，为了消除正负误差相抵，所以我们定义所 有目标输出和实际输出的误差平方和的一半为E。（因为平方的求导会出现2，所以这就是取一半的原因，这样2×(1/2)会使系数消失。）

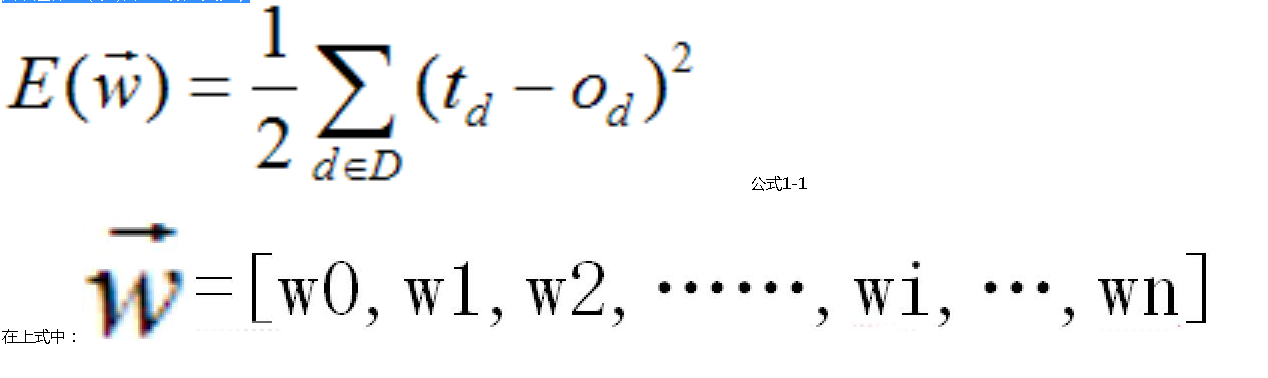
           公式1-1

在上式中：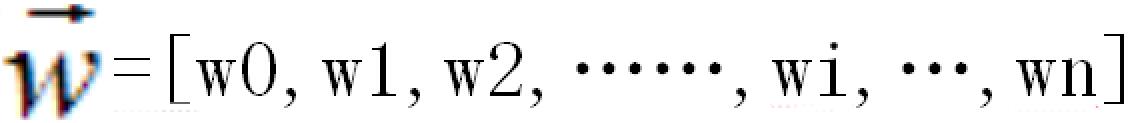

拿 我们这章第一个例子，单个神经元的房子预测神经网络模型为例，不难理解：Od=x0*w0+x1*w1+…xn*wn+b，结合前面的分析可知，x0， x1，。。。。。xn都是一个个的样本值， 是已知的。td也是已知的。这样看E是w0,w1,....wn和b的函数。我们的目标就是找到一组权向量（w0,w1,....wn和b）能使E最小 化。拿wi来说，我们可以画一条函数曲线：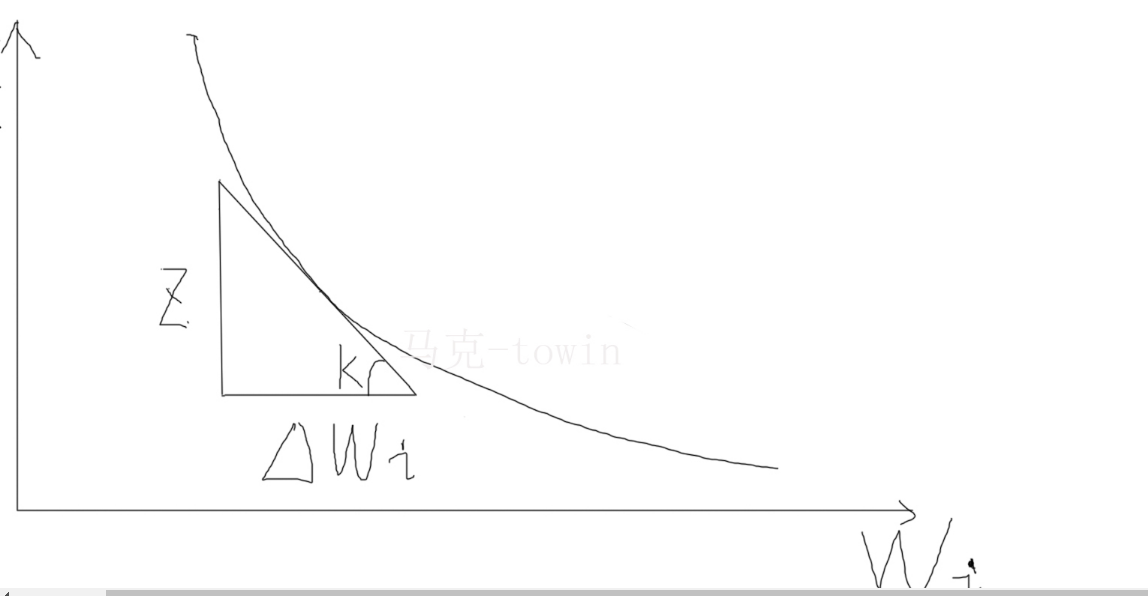





马克-to-win @ 马克java社区：防盗版实名手机尾号：73203。公式1-2：之所以是负号， 是因为图中斜率肯定为负值（因为是与x轴正向的夹角）。根据数学中梯度下降法。（delta wi为正，E越来越小）所以我们有下面一个业内著名的式子：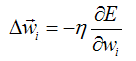








            公式1-2

伊塔就是著名的学习率，代表纵向（E方向）的变化幅度。（keras optimizers 默认学习率是0.01）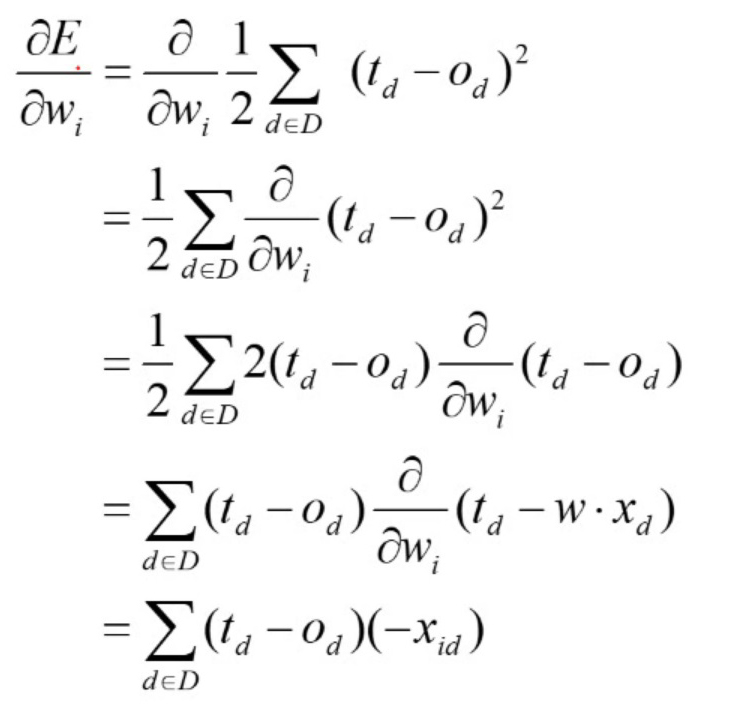

式子中：td已知，xid已知，od是输出，是可以计算出来的
代进公式1-3：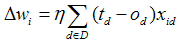








    公式1-4

公式1-4就是大名鼎鼎的delta rule（规则）
以上的式子推导是根据批量学习。但理论和实践中，我们也用逐步学习法（也就是不用通过所有样本点的求和，简言之， 求和号直接省略）

在前面上一段，我们提到：所有的权向量w都从一个很小的值开始，比如零，通过变化，最后让E达到最小。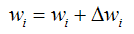






        公式1-5 
拿我们这章第一个例子，单个神经元的房子预测神经网络模型为例，Od=x0*w0+x1*w1+…xi*wi+.....xn*wn+b
来帮助理解以上的两个式子：公式1-4和公式1-5。根据此以上两个式子：我们的神经网络源代码自 己就能写出来。所有的权向量w都从一个很小的值开始，比如零。td，od， xid和伊塔的值都有，delta wi就能算出来。马克-to-win @ 马克java社区：新一轮wi就能求出来。接着再循环往复，直到最后计算出td和od一样，这时，delta wi就恒定为零了，Wi也就都求出来，这不就是我们训练的目的吗？全部到此就结束了，如果实在td和od的差距始终不能为0，那循环到一定轮数也就结束 了。